「人生的課題,如果你沒有學會處理,它就會一而再、再而三的讓你練習」…其實也沒那麼嚴肅啦,只是小時候沒學好,最近讀論文的時候一直碰到馬可夫鏈…讓我覺得很卡,於是想說花一些時間把這個關節打通。我希望用一些淺顯易懂的文字寫一些老嫗能解的馬可夫鏈概念(千萬不要像維基百科寫得像天書般),這就是邊學邊寫的最高境界吧,我想!

▲當我聽到「馬可夫鏈」的時候,總會想像一條長長的鏈子,鏈住馬的頭@@
正文開始
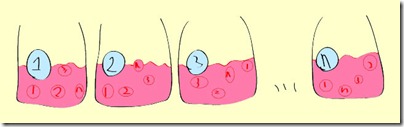
我們想像有一些加以編號的桶子,每個桶子裡面裝著數顆編號過的球,如下圖所示:
接下來玩法是這樣的,例如我們先在2號桶子中抽到3號球,於是我們就跑到3號桶子再抽一顆球;我們發現3號桶子抽出來的球是5號,於是又跑去5號桶子抽…總之從任一個桶子中抽出球的號碼,決定著接下來目的桶子的號碼,然後一直抽到沒完沒了(或某個次數),如此所形成的連續動作就是馬可夫鏈!
到這裡已經講完馬可夫鏈了,應該有如醍醐灌頂的感覺吧!那我們接下來看看,這樣的一條鍊子有什麼特別的呢?
馬可夫鏈的特色
馬可夫鏈最主要的的特色在於「下一個狀態決定於上一個狀態裡的機率」,以上面桶子抽球的例子來說,第k次抽球的桶子決定在第k-1次所抽出來的球(與前面抽球的機率都沒有關係)。此外,在同一個時間,馬可夫鏈只會有一個狀態,我們舉下一個例子:慈善賭場中有一個賭徒,身上只有一塊錢,每賭贏一次多一塊,輸一次少一塊(因為是慈善賭場,輸到負的還可以繼續賭XD)。
這樣也構成一個馬可夫鏈,第k次賭博身上所剩的錢,決定在第k-1次身上的錢&輸或贏,所以我們若知道第k-1次身上有10塊錢,就可以推論第k次輸了的話身上剩9塊錢,贏的話會有11塊錢。此外,我們還可以發現,狀態是可能來回循環的,例如可能會重複回到「一塊錢」的狀態。但是如果是三度空間以上的馬可夫鏈,狀態會離原點越來越遠(雖然不一定沿著固定方向)。
總而言之,馬可夫鏈有以下兩點特色:
- 在任何週期,系統中的事件只存在於一種狀態內。(每一局身上的錢只有一種狀態)
- 事件由一種狀態轉換到另一種狀態時的機率,決定於前一週期。(第k局加減的錢由第k-1局的機率所決定)
計算馬可夫鏈
一般而言,我們會使用轉移圖來了解馬可夫鏈狀態間的轉換,再搭配矩陣來計算馬可夫鏈的數值。一開始我們可以使用樹狀圖來分析馬可夫鏈,如下圖:

▲以上三張圖都在表示同樣結構的馬可夫鏈,a1, a2, a3 為三種狀態,而互相轉換的機率標在線上
我們都會使用矩陣來進行馬可夫鏈的計算,透過反覆的計算,例如計算第k步時停留在a1狀態的機率,達到一個程度的預測。
總結
馬可夫鏈的應用相當多,可以用來進行物理中排隊理論或統計學的建模,此外也可以應用在人口、生物觀察上(估計的繁殖或死亡狀態)。最值得一提的是,基於馬可夫鏈發展出狀態非顯而易見的隱藏式馬可夫模型(HMM)大量的被應用在辨識技術上,如語音辨識與文件切割等,這也是為什麼馬可夫鏈重要的原因。
參考資料:
- 馬可夫鏈的簡介:這是一篇從概念講起馬可夫鏈的文章,雖然後面寫得有點讓人想飄走,但是可以對馬可夫鏈有個概觀的了解。
- Ch 10 馬可夫鏈.ppt:朝陽科大資管系李朱惠老師的上課教材,使用例題介紹馬可夫鏈的運算

讀者回應 ( 9 意見 )
訂閱張貼留言 (Atom)
Thank you so much!!!!!
It is easy to understand and it helps me a lot!!
I cannot understand my text book but i can understand yours.
Anyway thanks a lot!
寫得真好!!!!
謝謝您的解說。
機率讀到這邊,有點不是太懂Markov Chains在說什麼,
上網搜尋就看到您寫的文章。
Very nice and very clear.
Thank you very much.
哈哈哈哈哈 用鏈子鏈助馬頭的圖也太逗趣了吧XD
謝謝分享心得
哈哈, very good.
thanks for explanation, it helps
你這文章寫得好。能再寫一篇白話談HMM的文章嗎?
淺顯易懂!謝謝您
張貼留言
如果沒有帳戶,建議使用「名稱/網址」留言喔^^